他写了一本专业数学书，竟然公开挑战整个数学界！

《复分析：可视化方法》用一种真正不同寻常的、独具创造性的视角和可以看得见的论证方式解释初等复分析的理论，公开挑战当前占统治地位的纯符号逻辑推理。作者通过大量的图示使原本比较抽象的数学概念，变得直观易懂，读者在透彻理解理论的同时，还能充分领略数学之美。

《复分析》的出版当年在数学界曾经引起过不小震动，主要原因是它的写法可谓独树一帜，在数学圈可谓不可替代。

来源 | 《复分析：可视化方法》作者 | [美]特里斯坦·尼达姆译者 | 齐民友

本书作者特里斯坦·尼达姆是知名数学家，物理学大家罗杰·彭罗斯是他的导师。说到本书，彭罗斯的喜爱之情溢于言表。

本书译者齐民友是国内著名数学家，除了淋漓尽致地展现原书的精髓，齐老师还耗费了不少心血为读者加餐——通过译者注扩展知识，进一步增强了图书的趣味性和知识性。

透过两位大家，你能深刻地感受到数学之美。豆瓣读者 @yang_bigarm 就以“此书让我理解了高等数学之美”为标题写了一篇推荐文章，摘录一段如下。

偶然之间发现了这本《复分析：可视化方法》，真是如获至宝啊！作者完全从几何直观的方面来解释复变函数中的相关定理，再没有复杂的级数和冗长的计算（记得译者在后记里说这本书甚至没有提到外耳斯特拉斯的名字，真是奇迹），只有清晰直观的图像和几何变换，很多以前莫名其妙的定理、结论就这样拨云见日了。再者，作者还把复变里面的概念和物理结合起来讲，比如莫比乌斯变换和洛仑兹变换之间的对应、零极点和磁场的对应等，让我从另一个层次对物理知识进行了再认识。

| 以下内容来源于书中前言部分

已知的各种理论, 时常可以用不同的物理概念来描述, 而它们做出的一切预测可能都是等价的, 因此它们在科学上没有区别. 然而, 当试图从那个基础走向未知世界时, 这些理论在人们心理上则是不同的. 因为不同的观点可能会提示做出不同的修正, 所以在企图了解尚未被理解的事物时, 由它们产生的假设并非是等价的.

R. P. Feynman [1966]

1一个寓言

假想有一个社会, 在那里, 鼓励（甚至是强迫）到了一定年龄的公民去读乐谱（有时还要谱曲）, 这一切都是令人尊敬的. 然而这个社会有一个非常奇怪且令人苦恼的法律（几乎没有人记得这个法律是怎么来的）——禁止听音乐和演奏音乐!

在这个社会里, 虽然音乐的重要性是被广泛承认的, 但是由于某些原因, 音乐并没有被广泛地欣赏. 可以肯定, 教授们在起劲地揣摩巴赫、瓦格纳等人的伟大作品, 他们尽其所能地向学生们传授他们在这些作品中找到的美丽的含义, 但是如果劈头劈脑地问问他们“这究竟有什么意义”, 他们只能无言以对!

这个寓言里, 立法禁止学音乐的学生直接从“声音的直觉”去体验与理解音乐, 这明显是不公正不合理的. 但是在我们的数学家社会里就有这样的法律. 这是一条不成文的法律. 虽然轻视它的人也还可能发迹, 但是这是一条法律, 那就是：禁止数学成为可视的!

很可能当一个人随便打开一本关于随便什么主题的现代数学教材时, 他面对的就是抽象的符号推理, 与他关于实际世界的感官经验完全脱节, 尽管他正在研究的现象时常是借助于几何（可能还有物理）直觉才发现的.

这反映了一个事实：近几百年来形象思维在数学中的名声被玷污了. 虽然伟大的数学家们从来也不在意这种风尚, 然而“街头巷尾的数学家们”直到前不久才接受了几何的挑战.

这本书将用一种新的、可以看得见的（即可视化的）论证方式解释初等复分析的真理, 公开地向当前占统治地位的纯符号逻辑推理叫板！

2计算机

对几何学的兴趣之所以又重新升起, 部分是由于广大群众都能使用计算机来画出种种数学对象, 也可能是由于与此有关的对混沌与分形理论的狂热的兴趣. 本书则主张比较清醒地把计算机作为几何推理的辅助.

我一直鼓励读者这样来看计算机：把它比喻为一个物理学家的实验室——它既可以用来检验关于世界构造的现有观念, 又可以用来发现新现象, 从而要求用新的观念做出新的解释. 我在全书中都建议这样来使用计算机, 但是我刻意避免给出详细的教导. 理由很简单：数学观念是长存的东西, 而几乎很少有比计算机硬件和软件更加转瞬即逝的东西了.

尽管如此, “

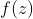
”程序仍是当前可视地探讨本书中各种观念的最好工具, 可以从Lascaux Graphics公司的网站免费下载其试用版. 如能使用诸如Mapler®或Mathematicar®这种多用途的数学引擎, 有时也是有好处的. 然而我想强调一下：不使用计算机也能完全理解全书.

3本书是在牛顿的“创世纪”中生成的

1982年夏天, 我在韦斯特福尔著名的牛顿传记（Westfall [1980]）的鼓舞下, 用功研读了牛顿的杰作《自然哲学的数学原理》（Philosophiae Naturalis Principia Mathematica, Newton [1687], 以下简称《原理》）. 诺贝尔物理学奖得主钱德拉塞卡（S. Chandrasekhar）的书（Chandrasekhar [1995]）追求的是完全展示牛顿在《原理》中提出的各种结论中所蕴含的自然本性, 本书则是着迷于牛顿的方法.

众所周知, 1665年出版的牛顿的微积分的最初版本和我们现在学的微积分很不一样：它的本质是幂级数运算, 而牛顿把对于幂级数的运算比喻为在算术中运用十进制小数展开式. 符号演算——就是现在每一本标准教科书上的那种微积分的讲法——通常是与莱布尼茨的名字连在一起的, 牛顿虽然完全熟悉它, 却认为它对于自己只有附带的意义. 毕竟, 牛顿运用幂级数就能计算

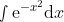
那样的积分, 像计算

一样容易. 请莱布尼茨也来试试这件事！

人们不甚知晓的是, 到了1680年左右, 牛顿对这两种方法都不再着迷, 那时他着手撰写微积分的第3种版本, 并以几何为基础. 这种“几何微积分”正是推动牛顿的《原理》走向辉煌的物理学的数学动力.

我在掌握了牛顿的方法以后, 就立刻在我教微积分入门课程中试了试自己的身手. 可以举一个例子来帮助说明这是什么意思. 我们来证明, 如果

, 则

. 如果我们让

增加一个小量

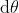
, 则

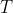
也将增加一个量

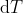
, 如下图所示. 要想得出结果, 只需注意到, 当

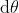
趋向0时, 其极限情况将是：图上的黑色三角形将最终相似于阴影三角形[练习]. 所以极限将是

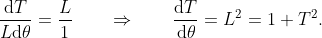
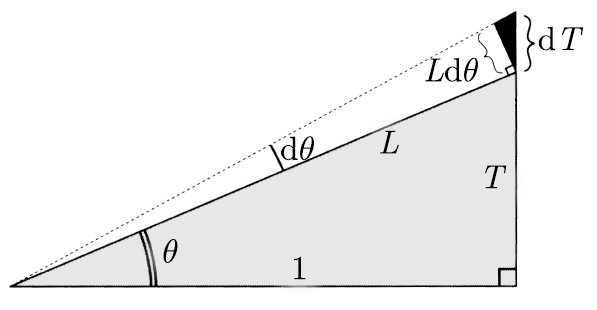
后来我才逐渐看到这种思维方式可以多么自然地用于复平面的几何学——那是在发现复平面几乎300年后的事了！

4怎样读这本书

为了使这本书读起来有趣, 我一直想把它写成好像向一位朋友面对面地解释其中的思想. 相应于此, 我也一直试图使你（读者）主动参与展开这些思想. 例如, 我在论证进展中, 时常有意地放上一两块逻辑的垫脚石, 放得相当远, 你需要停一下, 轻快地从一块石头跳到另一块石头. 这些地方都注上了“[练习]”标记；它们通常只需要做一点简单计算, 稍微想一想就行了.

这样就进到真正的习题, 它们放在每一章末尾. 我相信, 求解一个问题最本质的前提是有一种愿望要去找到解答, 所以我尽力给出一些能激起好奇心的习题. 这些习题比通常所见范围广得多, 而且在其中又时常会确立一些以后在正文中会自由用到的重要事实. 我一方面避免了那种从头至尾就只是例行计算的问题, 并且相信在求解这些问题的过程中, 读者会自动地发展出恰当的计算技巧. 另一方面, 在大量习题中我的意图正是要表明几何思维时常可以代替冗长的计算.