中世纪的科学家帮助发明了一个全新的物的世界......

摘自:《物的理论》
作者:托马斯·内尔
译者:蓝江
第十章 中世纪的物(一)
我们常常认为在“中世纪”或所谓的“黑暗”时代没有发生任何事情,但中世纪的科学家帮助发明了一个全新的物的世界。以前没有人梦想过对速度、运动或颜色进行量化,然而今天看来,由于这几个世纪所发生的事情,这是很自然的。早期的内敛科学建立在古代知识的基础上,并在决定性的问题上与之决裂,形成了现代科学革命和我们当代对物的理解。历史学家经常把牛顿誉为现代科学的天才,但牛顿所写的很多东西都是建立在中世纪的科学家所做的工作基础上或综合而成的。
在接下来的两个历史章节中,我想说明内敛物是如何通过这一时期的四个关键科学实践出现的:运动学、动力学、无限的数学和实验方法。我在这几章中的论点是,这四种科学都表现出运动的张力模式。
本章首先探讨了关于运动物的两门科学:运动学和动力学。运动学研究运动的形式,而动力学研究运动的原因。两者都奇妙地描述了这些新物体的可变性和张力性质。
一、运动学
运动学是对运动物的模式、轨迹和变化率的研究。然而,在安德烈·马里·安培在他的《科学哲学论》(1834年)中正式将其称为“运动学”之前,它被称为“形式的纬度”研究。学者们用 “纬度”一词来描述一种形式随着时间的推移而变化的程度范围。在整个中世纪,有几种关于这些纬度的理论。在下面的内容中,我想追溯这些理论的历史出现,这样你就可以看到它们是如何在对象的范围内变得越来越广泛,在张力运动中变得越来越精确。
1. 形式的纬度
第二世纪的希腊医生盖伦在他的《微观世界》第二卷中首次提出了“纬度”或“形式的逐渐改变”的概念。他发明了这个术语来描述健康和疾病状态之间的渐进连续性。盖伦用来表示纬度的希腊语是πλάτος,platos,意思是“平面”、 “表面”或 “宽度”,因为他把健康描绘成一个连续的表面。他在这张图上确定了三个区域。一边是最佳的健康状态,另一边是严重的疾病状态,中间是一个中性状态。他没有把健康看作是一种离散的算术状态,而是把它看作是一种连续的几何状态,其程度不断变化。
尽管很新颖,但盖伦的纬度概念仍然局限于一个单一主体的变化。我的意思是,这些变化只是一个主体在一定程度上受形式影响的变化。例如,主体可以更健康或更不健康,但疾病的形式本身并没有改变。盖伦和那些跟随他的人仍然不愿意承认形式本身发生了变形。阿维森纳的“混合论”、托马斯·阿奎那的“实现论”和方丹的戈弗雷的“继承论”也是如此。然而,随着纬度的“加法理论”的出现,这一切在13世纪发生了变化。
2.加法理论
纬度的加法理论是第一个承认形式的纬度适用于形式本身的理论。这一理论很早就被根特的亨利和米德尔顿的方济各会神学家理查德所辩护。米德尔顿的工作随后影响了邓·司各特、奥卡姆的威廉、彼得·奥里尔(Peter Auriol)、里米尼的格雷戈里(Gregory of Rimini)和牛津大学的计算者托马斯·布拉德沃丁(Thomas Bradwardine)、威廉·海特伯里(William Heytesbury)、理查德·斯温斯海德(Richard Swineshead)和约翰·丹伯顿(John Dumbleton)。
根据加法理论,数量和质量都有自己的纬度,在这些纬度中,“根据它们的性质和本质”,可以区分出连续的程度,正如根特的亨利(Henry of Ghent)写道。他说,“我们可以看到,在这个问题上,一个物体的大小和一个完美的程度之间没有任何区别。”根特所说的“大小”是指数量,而“完美”则是指质量。对根特来说,一个形体的质量变化可以像数量的变化一样,以系列的形式彼此相加。质的和量的系列都可以无限地增加。“如果我们所说的形式的可以无限大地完善,那么任何通过加法的增加,被认为是绝对的和简单的,都可以进行到无限大”[7]。米德尔顿同样认为,以前的学者认为力的增加是一种质量,可以通过加法像质量的数量一样增加。
邓·司各特对这些观点进行了补充,认为质量度就像一把尺子的纬度。每一个度数都是所有低度数的总和,因此是相加的。例如,司各特写道,一堵墙的白度可以不断增加而不改变墙的数量方面。或者如奥卡姆所说,“有些强度的增加是通过将一个部分添加到另一个部分来完成的;第二个部分与第一个部分构成一个单一的东西,但它并不因其地点和位置而与第一个部分区分开来(因此,当一个完全是白色的身体变得比原来更白时就是这样)。”
在公元14世纪,牛津大学的两位计算学家丹伯顿和斯温斯海德提出了一个关于质变的 “测量”系统的观念。他们认为,人们可以在同一个连续的纬度上测量定性的变化程度和定量的变化程度。他们设想,如果他们以同样的方式对待所有的质量,就像他们用数量上的距离来映射物体的运动或速度一样,这将是可能的。通过同时协调物的位置变化和其位置间的变化率(速度),他们提出了平均速度定理的第一个表述。该定理指出,如果一个以恒定速度运动的物的速度是被加速物的最终速度的一半,那么该物在相同的时间内与被加速物的距离相同。
他们的新测量系统区分了均匀的速度(latitudo uniformis)和非均匀的速度(latitudo difformis)。这种方法也促使他们以类似的方式绘制其他质量变化,如光照、热量和密度。与亚里士多德相反,他们认为质量和数量变化的速度可以在任何特定的瞬间确定。这就是他们所说的物体的“瞬间速度”。正如斯温斯海德所说,“每一度的速度(即定性或瞬间速度),都对应着一个线段的距离,假设在这一度的时间内有一个运动,就会有一个线段的描述。”
对于所有牛津大学的计算者来说,纬度是一个同质的连续体,人们可以把它表现为一条线,上面唯一的差异是长度的差异。根据美国科学史学家艾迪特·西拉(Edith Sylla)的说法,这一理论为:
为质量的量化提供了更好的物理基础,因为纬度对应于物体某一点或某一瞬间的质量的强度或程度,而不仅仅是质量在其延伸或时间上的一些变化。速度的纬度被想象成一条线。速度纬度的相等部分对应于速度的相等差异。
3.几何理论
关于形式纬度的最终和最精确的理论被称为“几何理论”,因为它把物体的质与量的同时变化绘制成几何图形。历史学家有时将此归功于中世纪法国神学家尼克尔·奥里斯姆(Nicole Oresme)。然而,根据美国历史学家马歇尔·克拉吉特(Marshall Clagett)的说法,是一位名叫乔瓦尼·卡萨里(Giovanni Casali)的意大利方济各会士在1346年的《论改变运动的速度》(De velocitate motus alterationis)一书中首次描述了这一思想的基本内容。斯温斯海德也含蓄地提出了几何理论,他将一个地区的几何长度和宽度与记录量变(他称之为 “外延”)和质变(他称之为“内敛”)的线条进行了比较。
在他的《论性质和运动的配置》(De configurationibus qualitatum et motuum)(约1350年代)一书中,奥里斯姆还引用了亚里士多德用线来表示时间段;格罗塞特用线来想象“光的强度”;以及欧几里德注释家乔瓦尼·坎帕尼(Giovanni Campani)说,人们可以通过线、面或体来想象任何连续的东西,作为他想法的先导者[14]。奥里斯姆借鉴了这些思想,使用经纬度的几何坐标来绘制物体的内敛和外延变化的面积和速度。
奥里斯姆的作品在细节和清晰度上也大大优于他的任何前辈。德国科学史家安丽斯·迈尔(Anneliese Maier)将“奥里斯姆的图形表现方法”描述为“无疑是十四世纪最具独创性的成就 ”[15]。他的伟大创新是将物的所有变化视为两个几何坐标中的连续运动变化。
奥里斯姆从三个相关的历史思想中发明了我们可以称之为“内敛几何”的东西。首先,他采用了亚里士多德的概念,即改变总是涉及到一个连续的运动。亚里士多德称其为“纯质”。然后,奥里斯姆借鉴了欧几里德的信念,即人们可以把所有连续的物想象成几何物体。最后,奥里斯姆借用了牛津大学计算者的概念,即人们可以把所有的质变想象成连续的几何线。把这些放在一起,奥里斯姆出色地指出,只要“每个可测量的物是一个连续的量”,它也必须有连续变化的量。他把质和量的变化想象成两条直线,在它们通过时间的关系中追踪一个几何形状。
奥里斯姆把这些新的物,或他所谓的“内敛物”(rei intensibilis),视为由两个不断变化的维度组成的几何表面或区域。第一个维度是追踪物体的质变。他把这种质变的维度称为 “内敛变化”,因为它描述了一个物体如何变得更多或更少的质,如白度或牢固性。内敛变化,例如颜色的变化,对奥里斯梅来说,不是加法变化,因为它们没有部分。例如,如果你把白色栅栏涂成白色,它不会变得更白。然而,当篱笆上聚集了灰尘,它就会变得相对“不那么白”。在第一节中,我把这类有质量等级的物称为“序数物”。当奥里斯姆描述被说成是 “更多这样那样”,“更白”或 “更快”的东西时,他想到的也是这些类型的物。
奥里斯姆的几何图的第二个维度描绘了一个物体的数量变化。他把这种数量上的变化称为“外延变化”,因为它描述了物体在空间和时间上如何获得或失去部分。外延变化,比如把两个一英寸的积木堆在一起,形成一个两英寸高的积木,是加法的。这些是我在前几章中称为基数物的类型。
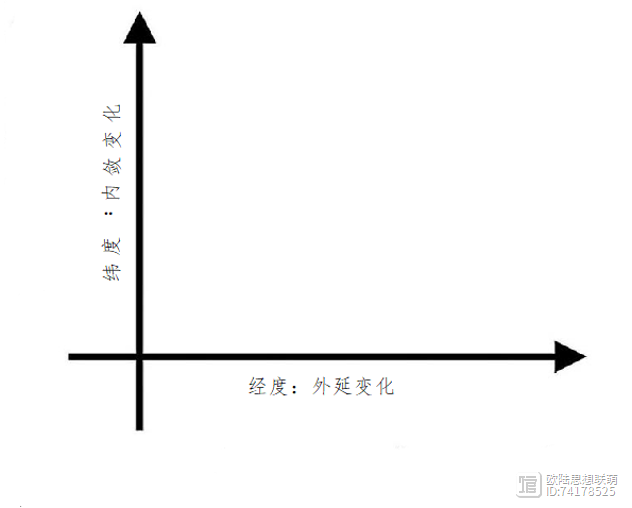
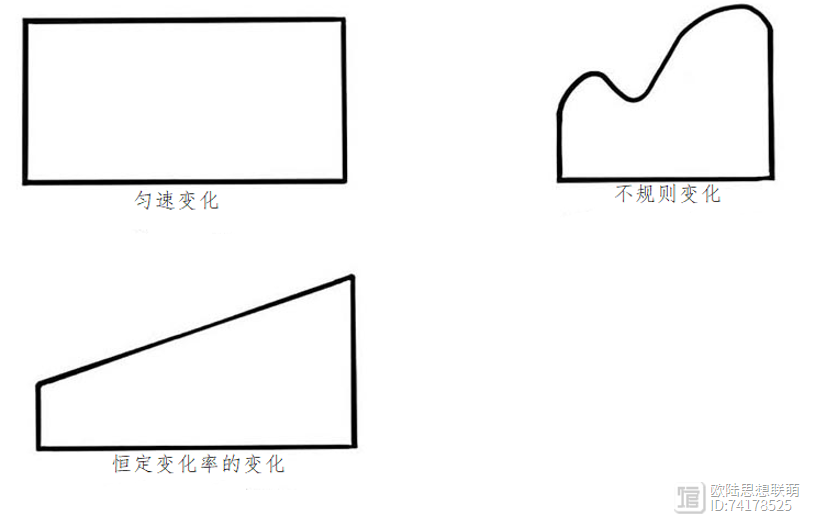
奥里斯姆将每一种序列沿着其几何线绘制出来。他沿纬度线画出内敛变化,沿经度线画出外延变化。然后,他在第三条线上绘制了每种序列之间的变化比例。绘制这种协调继承比例的变化率,可以画出一个几何图形或区域,例如一个正方形或三角形。
使用这种方法,奥里斯姆可以通过映射其作为经度的时间变化与作为纬度的速度变化的比率,计算出一个物体所走的距离。如果变化率保持不变(uniformis),得到的数字看起来就像一个正方形。如果变化率以恒定的速度变化(uniformis difformis),它看起来像一个三角形。如果变化率以可变的速度变化,它看起来更像一条曲线或不规则的多边形(uniformis difformis difformis)。然后,人们可以按照几何学的规则定量地测量这些形状所产生的面积。
然而,奥里斯姆的几何方法不同于笛卡尔的平面直角坐标系,因为它没有在网格上绘制 “点”,而是将线条画到几何区域。奥里斯姆的几何方法的重要性和新颖性在于,它保持了异质性的质变和量变之间的张力。他的图表并没有把两者统一在一系列的点上,而是把它们的轨迹描画成图形。

4.内敛物
在讨论的最后,我想澄清一下中世纪运动学与我的“内敛物”概念的关系。我还想说明运动学是如何遵循运动的张力模式的。
我所说的“内敛物”与奥里斯姆等人所说的物的“内敛运动”或“非加法性”变化不同。在我的用法中,内敛物既不是单独的内敛-基数物,也不是外延-基数物,而是在同一平面上同时绘出的这种物体的变化系列的比率。比率本身是由序数和基数序列之间的协调张力所构成的新的第三种内敛物。有了内敛物,人们不再能一劳永逸地测量一个物,而必须进入一个连续的测量过程,跟踪物的变化和变形。
在中世纪,进入知识的前台的是在测量行为中发现的变化的序数的质和基数的量之间的紧张关系或比率。在中世纪,正如法国哲学家和数学家吉尔·夏特莱(Gilles Châtelet)所写的那样,“测量”首先必须被理解为一种认识行为,是对某种程度的可理解性的阐述——这里是思想或多或少迅速地对空间的理解——以及从整体中提取的部分并置的节奏。
在本质上,内敛物是一个通过运动过程制造的纯粹的相对物,或亚里士多德称之为“纯粹变化”。计量单位、计量行为和计量对象不是独立的,而是被视为单一内敛物的三个方面。对内敛科学来说,物本身的活动成为一个新的研究对象。
这些物有两个主要的张力方面。第一个是物的质与量方面的张力。在第二章中,我说过,一个“物”是一个可变化的过程,有一个定性和定量的方面。抽象的基数物的局限性之一是,它们把物当作没有质的东西。内敛科学之所以如此吸引人,就是因为它们试图把物不断变化的质与量结合起来,以获得对物的更全面的认识。这种质与量之间的第一种张力关系不仅是物本身的真实物质性的张力关系,而且是科学利用新的绘图和制图技术在物理上努力坚持的东西。

第二种运动张力通过对每个物的质与量维度的变化进行图解,将一整个序列的物固定在一起。
内敛物被保持在张力中,内敛型和外延型。为了使事物持续存在,它们需要在其变化的质与量之间保持相对稳定的比例。否则,它们就会崩溃。[20]中世纪研究内敛物的科学家明白这一点。他们的工作为后来的思想家如伽利略、布里丹、哥白尼和牛顿奠定了基础,我将在下一节说明。

二、动力学
这一时期的第二门内敛科学是动力学。动力学是对运动物体变化原因的研究。科学家把这些原因称为“力”,如“冲力”、“惯性”、“持续力”(conatus)和“作用力”(vis impressa)。这些力描述了运动中的作用物体和反作用物体的比例变化。运动学的重点是单个物体内的变化率,而动力学的重点是物体整体运动的原因。
我在这一节的论点是,动力科学是从运动学的研究中产生的,并依赖于相同的运动内敛模式。动力学还将对内敛物的研究从运动学的理论和图形模型扩展到物理学、天文学、光学、生物学、计时学、水力学和磁学等实验科学。这些新的科学也需要新的测量技术,如钟摆、望远镜、光学镜头、显微镜、时钟、真空泵和指南针。我想说明的是,这些技术也遵循了塑造内敛物的运动张力模式。
1. 大地动力学
动力学最早的领域之一是研究地球运动的原因。为什么事物在某种因素的作用下会不断运动?亚里士多德认为,小股空气推动着扔出去的标枪前进,就像他想象的那样,上帝,或者他所谓的“最终推动者”,不断地推动万物前进。这是对因果关系和运动的一种古老的离心式理解,在这种理解中,一个单一的静态中心引起了周边的运动。
然而,在整个中世纪和现代早期,出现了一种对运动原因的新理解。它被称为“力”,或希腊语中的rhope,由六世纪基督教神学家约翰·菲洛波努斯提出。对菲洛波努斯来说,力不是单向的或同质的,而是与介质的摩擦成反比的变化率。法国牧师让·布里丹最终在欧洲推广了力的概念。[22]然而,直到伽利略的作品和他在1602年左右对摆(pendulum)的最初研究,力的概念,或他所说的冲力,才在动力科学中得到实际应用。
(1)摆
摆具体地展示了物的力量,并可以对其进行测量。根据伽利略传记作者和学生维森科·维维亚尼(Vincenzo Viviani)的说法,伽利略通过协调他的脉搏和比萨大教堂吊灯的摆动运动,发现了钟摆运动的规律性。[23] 伽利略是第一个观察到,尽管移动的距离不同,但绕着一个支点摆动的重物从一边到另一边所需的时间是一样的。钟摆表明,摆动之间的加速率与振幅的减少成正比,慢慢减少。
伽利略还认为,摆动的周期与绳子的长度近似相关。摆锤摆动一次所需的时间,其平方等于弦的长度。更令人印象深刻的是,伽利略据此推断,在没有空气或摩擦的情况下,最初的“重物下落获得足够的推动力,使其返回到同等高度”。
摆的运动模式是张力性的。枢轴点和摆动的重物之间的绳子有一种张力。重物的运动和减缓它的摩擦力之间也有张力。由于重物不会回到人们释放它的准确位置,伽利略推断,一定有其他力量对运动的重物起着张力作用,使它慢下来。摆的伟大之处在于,它是一个可重复的机械装置,人们可以用它来相对准确地测量力。
摆第一次使运动的力量和惯性的反作用力之间的张力和比例关系变得可见和可测量。它帮助创造了一个新的动态物,由速度的不可分或“内敛变化”与振荡的可分的“外延”的量之间的运动张力或相关性组成。这样一来,力的动态物的发现与摆的物质性和运动学紧密相连。没有它,科学家们只能接触到奥里斯姆的更多理论性的图表。摆是首批通过实验测量动态量的仪器之一,如运动物体的加速度、振幅和周期性的变化率。
2. 天体动力学
另一门重要的内敛科学是天体动力学。天体动力学研究天体的因果关系,就像大地动力学研究地球的力量一样。在整个现代欧洲科学的兴起过程中,古代的同心球和不变的形式的地心模型越来越不受青睐。科学家们想知道是什么导致了天体的运动方式。现代天文学家提出了这样一个观点:天体的运动是由在地球上起作用的相同的吸引和排斥的张力作用在一起或分离的。这是一个巨大的变化,因为古代人认为天体遵循完全不同的规律。[25]现代科学家看到的不是天地之间的根本区别,而是同一个物理世界的两个方面之间的张力。
(1)望远镜
望远镜的发明极大地促进了哥白尼的日心说。它第一次使行星、卫星和彗星的动态和张力运动清晰可见。望远镜本身也通过张力运动来工作。
因此,我们可以确定天体观测的三个动力学阶段。史前的观测遵循的是向心模式,光线从天空的外围聚集到眼睛的中心。古代日晷通过创造一个固定的物,将其影子投射到周边的表面上,从而遵循一种离心运动。现代望远镜有一种新的张力运动,使用凹凸透镜来折射、收缩和弯曲光流到一个焦点上。这使得大的东西看起来很小,而远的东西看起来很近。通过在管子的一侧结合凸透镜,在另一侧结合凹透镜,望远镜可以捕捉光线,并在收缩(凸)和扩张(凹)的光波之间创造一种光学张力。
由于镜片的不完美和聚焦发散光波的过程,这种光学张力也产生了一些视觉像差和光的衍射。在衍射光波汇聚的地方,人们可以看到聚焦的天体。在它们发散的地方,人们看到光环和光圈。这样,望远镜的衍射通过光波的张力使放大和变形成为可能。
和摆一样,望远镜是一个张力物,它使协调天体的质量变化与它们在空间和时间的数量变化成为可能。其结果是一个全新的内敛型天文科学。

(2) 天体
开普勒、伽利略和牛顿都用望远镜来支持地球以其轴心旋转的观点。这些天文学家想象的是天体之间更多的三角和多边形关系,而不是完美的同心圆。
对开普勒来说,天体的三角力量使数学、几何学和所有存在中的“神圣比例”或“黄金三角”成为可能,这并非巧合。[26]对开普勒来说,自然界的语言是数学,而上帝的名字是神圣的多边形。上帝把行星固定在一起,但他的力量是复数的,而且是在乙醚的流体介质中间接的。对开普勒来说,行星的轨道在柏拉图实体的多边形形状中彼此保持张力:四面体、立方体、八面体、十二面体和二十面体。
对开普勒来说,天体运动不再是同心的,而是由上帝——几何学家——制造的运动的、和谐的几何图形的比例。天体之间的吸引和排斥关系采取了精确比例的形式,就像伽利略的钟摆运动定律一样。
(3)重力
牛顿把天体之间的这些吸引和排斥的拉力称为“重力”。在他的《自然哲学的数学原理》中,牛顿声称,科学的全部任务是研究运动现象并确定其因果关系。一旦科学家发现了变化物体的比例,其他人就可以把这些规律应用到所有其他运动中。
对于牛顿来说,因果关系的力具有双重功能。当一个物体处于静止状态时,它有一个静止的力(vis insita),可以抵制任何“试图改变其状况”的物体。当它处于运动状态时,它有能力从外部给其他物体施加和作用力。它是阻力,因为身体为了维持其目前的状态而反对所施加的力;它是冲力,因为身体不容易让位于另一个人所施加的力,而努力改变另一个人的状态。
对牛顿来说,重力是一种像液体一样的张力,它可以在物体之间作用,同时把它们固定在一起,又把它们分开。引力是“对中心的绝对力量,因为它被赋予了某种原因,没有这种原因,那些动力就不会在周围的空间传播”。
3.流体动力学
第三种关键的内敛科学是流体动力学。流体动力学根据空气和水等物体的内敛和外延变化率来研究它们。古代水系动力学的重点是通过运河、水渠、灌溉、水坝、水井和蓄水池将流体从中心源头移动到外围目的地。然而,现代流体动力学则关注流体彼此间的速度变化。
流体动力学对正方形和圆形之间的形式差异不感兴趣,而对正方形向圆形的连续过渡感兴趣。现代流体动力学利用技术创新,如显微镜和温度计来研究血液在体内的循环和水在管道中的速度。在流体内部,有一种叫做“压力”和“粘度”的吸引力和排斥力之间的张力。让我们看一下这些张力的两个例子,一个来自生物学,一个来自水文学。
(1)显微镜
1628年,威廉·哈维发表了《论心脏和血液的运动》,在理论上,哈维认为,血液从心脏穿过整个身体,返回,并循环流动。1661年,显微镜的发明证实了毛细血管的存在和哈维的理论。
显微镜的动能与望远镜的动能相似。两者都使用折射光的光学张力,都允许科学家在更高的放大率下观察物体。在盖伦的时代,科学家通过解剖不动的尸体获得解剖学知识。然而,显微镜使我们有可能观察到运动的身体之间的动态张力。然后,科学家们可以在这些身体中建立质量和数量变化的比率和比例。
例如,哈维只用了一个小手镜,就提出了一个全新的血压和循环的张力理论。相比之下,盖伦持有一个更加离心的理论,即血液在一个中心位置,即肝脏产生,然后单向分配到周围的四肢。在那里,身体会消耗它。对盖伦来说,心脏和肺只调节身体的温度,与血液循环无关。
然而,在哈维的模型中,不再有单一的离心式血液来源。相反,存在着动态的血液流动,在不同大小的动脉中被加压的张力推拉。当血液沿着动脉壁移动时,它产生了粘性、摩擦和压力。因此,他认为血液运动是动态的,对整个循环系统中的压力变化有反应。
哈维甚至能够通过把两个变化的系列物体放在一起来测量血液的流动。他估计,心脏每次跳动都会释放出八分之一的血液容量,心脏每天大约跳动一千次。这个血量乘以这个心率,等于比人体所含的血液还要多。因此,哈维推断,血液不可能每天都在肝脏中生成,但人体必须进行血液循环。
4.热力学
我想看的第四个也是最后一个动力科学是热力学。热力学是对热的研究,与流体动动力学有关,因为它也研究流体材料的压力、张力和变化率。热力学在使用现代仪器协调质和量的变化方面也遵循同样的运动张力模式。这门新科学的关键工具之一是温度计。
(1)温度计
温度计和气压计使科学家能够将两个变化的物体序列协调成一个新的内敛物。他们观察了一个加压管内液体的质量变化,并将其与管子上一系列等距的标记相协调。这两个系列之间的协调张力使一个新的比例变化的张力物成为可能。
这种仪器的最早表现是伽利略在1593年制造的温度计。伽利略将一根垂直上升的细管,上面有一个大的空玻璃球,连接到一个装满水的小花瓶。当上面的球的温度发生变化时,它将改变下面的水位的压力,使其在垂直管道中向上或向下移动。球的温度越高,压在液体上的张力或压力就越低,液体就会在管子里上升。
1611年,伽利略的学生桑托里奥·桑托里奥(Santorio Santorio)在管子的一侧增加了一系列的标记,以量化运动的情况。有了这个补充,伽利略和桑托里奥发明了一个新的内敛物,将流体的质量变化与标记的数量单位相协调。然后,压力、温度和体积的变化可以作为单一热力学物体内的非弹性比例变化尺寸联系在一起。
(2)波义耳定律
温度计和气压计使科学家们有可能对流体的可控变化率进行新的实验。流体和气体的温度很有趣,因为它们的变化是如此的成比例,而且与大气有更广泛的联系。把物体当作与环境隔绝的不变的整体是不够的。
波义耳定律是对这一思想的最重要的综合。爱尔兰自然哲学家罗伯特·波义耳发现这一定律,对于在固定温度下保持一定量的理想气体,压力和体积是成反比的。在固定温度下,对固定数量的密闭液体施加的压力越大,液体体积就越小。通过这种方式,波义耳展示了一个新的内敛物,由温度、体积和压力的同时比例变化组成,在一个不断变形的物体中。这些比例之间的张力使这成为一个内敛物。
三、结论
本章展示了一些最早的内敛物是如何通过运动学和动力学出现的。我的论点是,这些运动物体的科学沿着两个或多个协调的维度按比例测量变化。这就是为什么它们遵循我在前一章描述的运动的张力模式。
这一章并不是一部完整的内敛物的历史。相反,它的目的是让读者了解中世纪和近代的物在运动模式和测量工具上与古代的物有什么不同。
运动学和动力学仅仅是内敛物发明的核心的两门重要科学。还有两门科学在形成这些我想展示的新物体方面发挥了关键作用:无限数学和实验方法的创造。这些是我们在本节中关于内敛物的下一章和最后一章的主题。
- 0000
- 0000
- 0000









